Blue Heron Enrichment
Fun activities and ideas for STEM classrooms.
Monday 22 May 2023
Monday 10 April 2023
Friday 24 March 2023
Arithmetic Practice
Want to get better at addition, subtraction, multiplication or division? This simple tool can be really helpful:
https://arithmetic.zetamac.com/
Here is another simple flash card tool:
https://sergemister.github.io/mathpractice/
Go ahead, make your math muscles stronger! You can do it!
Monday 17 June 2019
Simple Machines
Fold and Cut Challenge
Did you know that it has been mathematically proven that any shape with straight sides can be cut with one cut, if the paper is pre-folded in the appropriate way?
Tuesday 11 June 2019
Wednesday 22 May 2019
Watering Plants With Microwaved Water - step one
What do you think of this?
To be continued... Look for another post.
Wednesday 8 May 2019
Geometry Dash Instructions
These are some on-line instructions, but I found them hard to follow.
I would recommend the YouTube videos by GriffPatch about how to make scrolling games in Scratch:
Here are basic instructions I created. The final project can be found here:
- Basic Geometry Dash
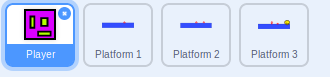
Make these sprites:
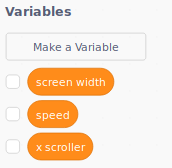
Create these variables for all sprites:
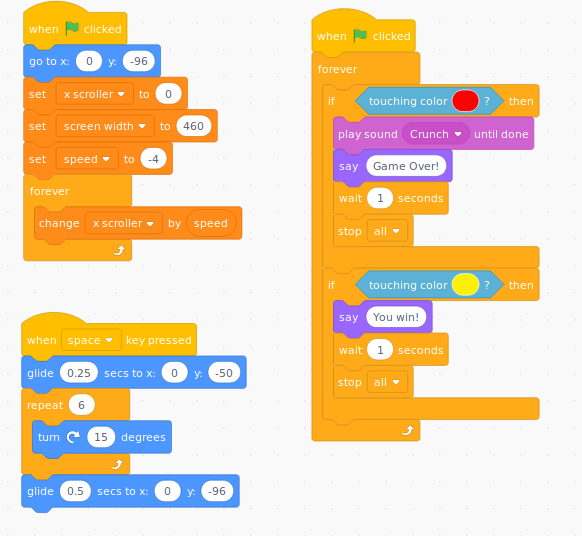
Add this code for the Player Sprite:
Add this code to the Platform 1:

I would recommend the YouTube videos by GriffPatch about how to make scrolling games in Scratch:
Here are basic instructions I created. The final project can be found here:
- Basic Geometry Dash
Make these sprites:
Create these variables for all sprites:
Add this code for the Player Sprite:
Add this code to the Platform 1:
Add this to Platform 3:
Subscribe to:
Posts (Atom)